Modeling word and morpheme order in natural language as an efficient tradeoff of memory and surprisal

Abstract

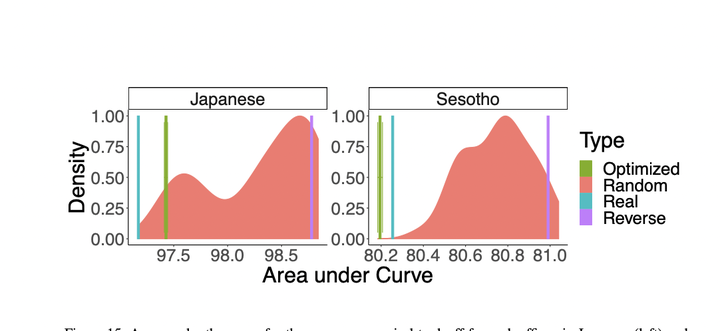
Memory limitations are known to constrain language comprehension and production, and have been argued to account for crosslinguistic word order regularities. However, a systematic assessment of the role of memory limitations in language structure has proven elusive, in part because it is hard to extract precise large-scale quantitative generalizations about language from existing mechanistic models of memory use in sentence processing. We provide an architecture-independent information-theoretic formalization of memory limitations which enables a simple calculation of the memory efficiency of languages. Our notion of memory efficiency is based on the idea of a memory–surprisal tradeoff: a certain level of average surprisal per word can only be achieved at the cost of storing some amount of information about past context. Based on this notion of memory usage, we advance the Efficient Tradeoff Hypothesis: the order of elements in natural language is under pressure to enable favorable memory-surprisal tradeoffs. We derive that languages enable more efficient tradeoffs when they exhibit information locality: when predictive information about an element is concentrated in its recent past. We provide empirical evidence from three test domains in support of the Efficient Tradeoff Hypothesis: a reanalysis of a miniature artificial language learning experiment, a large-scale study of word order in corpora of 54 languages, and an analysis of morpheme order in two agglutinative languages. These results suggest that principles of order in natural language can be explained via highly generic cognitively motivated principles and lend support to efficiency-based models of the structure of human language.